Emerald Education White Papers

The Unique Power of Playing Games in K-8 Math
WRITTEN BY STEVE LEINWAND
Imagine four students at a classroom table working on a twenty-problem practice worksheet. We see the students working alone, not talking or sharing. We are likely to see memorized rules and procedures being used to get twenty answers, with little challenge, great tedium and minimal feedback until a red number announcing the number correct appears on the worksheet. This all too typical scenario is the norm for math classrooms – a lot of mindless practice and regurgitation, little learning of concepts or opportunities to apply the mathematics, and not much challenge, fun, or excitement.
Now move next door where four students each have a subtraction template like the one shown and a single deck of 0-to-9-digit cards. The students pick cards, one at a time and each student enters the number on the card in one of the five subtraction boxes. Once placed in a box in the template, the number cannot be moved and the process continues until five different cards have been drawn and each student has a completed template with five different digits in the boxes. Today’s goal is to get the greatest difference.

Imagine where you might place a six if it’s the first digit drawn, or a 2? Think about the reasoning and strategies you might use and the incentive to compute the difference. Think about the discussion that can happen, both during play and after the greatest difference is determined.
Then think about just a few natural variations:
- Using those same five digits, what is the greatest difference you can get? How did you get it and how do you know it is the greatest difference?
- Suppose we change the game to addition or multiplication?
- Suppose that instead of greatest difference, we try for the smallest difference?
- Suppose we see who can get closest to a difference of 400 and then determine what arrangement of the five digits can get you closest to 400?
It’s not hard to imagine the energy and excitement among these four students. It’s easy to imagine the discussion about place value, how to get greatest and least differences and how your strategies must change when the goals change. And what a joy to see these students providing themselves with feedback, as they eagerly practice mathematical skills.
But it’s important to note that it’s the variations, like those suggested above or created by students, that make the gaming experience so rich. The variations maintain the core structure of the game, making it easier to jump right into a related, but different, version. The variations also make the game environment easily adaptable for both enrichment and remediation. In other words, games and their variations become engaging vehicles for differentiation by providing safe, low-floor entry points for all to play with success and simultaneously offering richer, deeper, and more challenging opportunities for some.
Adding on to the variation concept, there is a naturally occurring benefit of game play which is the fact that each time a game is played, it’s a different game. The cards drawn, or the dice rolled, result in new problems each time and possibly a different strategy. This potential for variety gives students many additional opportunities for practice with what could be a variety of problem types. Equally important, is also part of what makes games so engaging for students…it’s never the same game twice.
No one is arguing that all math worksheets should – or even can – be replaced by games, but the current dominance, and typical boredom, of one over the power and potential of the other represents a serious missed opportunity. We all understand that mindless practice of the same skill with little opportunity for differentiation on a 20-question worksheet falls well short of the potential for engaging games and their variations to be welcome alternatives in our classrooms and as components of our mathematics lessons.
From play to games to learning. The argument that must be made is the pathway from play, to playing games, to learning from games seems self-evident: We play because play is a human virtue. We play games because games provide varied, structured and engaging environments for play. And we learn from playing games because games have rules and structures and goals that can engage our thinking and reasoning, our motivation, and our need for social interaction. In fact, one of the great ironies of schooling is how the practice of playing games to engage and learn tends to decrease steadily and unfortunately from Pre-school on up through the grades, with far too many students paying an incalculable price for this missed opportunity.
So, let’s parse this out:
PLAY. To play, according to the dictionary is “to engage in activity for enjoyment and recreation.” Reading further, “play is an activity where children show their remarkable ability for exploration, imagination and decision-making.” In Mathematics for Human Flourishing, Francis Su argues that play, along with beauty, truth, justice and love, is one of five human desires. He links play to the virtues of community, hopefulness and perseverance and note that humans cannot flourish without play. How helpful and convenient it is that for many, mathematics is a playground of the mind. All of this explains why we play a lot in pre-K and K, but rarely is play a significant component of 1st grade math and beyond where test-prep drudgery prevails. To be blunt, and to the detriment of learning and engagement, we basically stop playing as school becomes unnecessarily serious.
GAMES. Once again, turning to the dictionary, we are reminded that games are inextricably linked to play. “Games are any form of play or way of playing; amusement; recreation, sport; frolic.” Games are “any specific contest or competition involving engagement, amusement, and rules.” My favorite, compliments of the Oxford Learners Dictionary, is that a game “is an activity that you do to have fun, often one that has rules and that you can win or lose.” In short, games are activities in which we play. Good games pique our interest, motivate us to engage, and offer an accessible environment for play. While some games are played individually, more games are interactive and social in nature, broadening the benefits of play.
LEARNING. And learning is the acquisition of skills, knowledge, understandings, and the dispositions that schools and homes are charged with developing. As we saw in the opening examples, there are many ways to foster learning. But clearly, focusing on play and on playing games embody many of the characteristics of effective learning: game players tend to be more motivated, more engaged with the task and with others, and often having a lot more fun.
“Yes, but…” we hear you saying. Doesn’t all this fly in the face of the dominant belief that learning is somehow supposed to be hard, rigorous, and dreary work, particularly in the test-driven environment that elevates skills and speed over fun, engagement, and deeper learning. Alternatively, it is worth considering that:
- The problem with the perception that work is good and play is a frill, is that it ignores basic human motivation and assumes that play doesn’t really engender learning.
- The problem with the perception that games are merely for entertainment, fun and play, ignores the intrinsic power of games to teach and reinforce and the fact that many games are extraordinarily rigorous.
- And the problem with the perception that learning emerges from listening and regurgitating just as powerfully flies in the face of what mountains of research tell us about engaged, minds-on, collaborative, goal-oriented learning.
On this hopefully compelling foundation, we overlay mathematics – recognized as a troubled discipline in many schools and in desperate need of vigorous invigoration of exactly the sort to which playing games lends itself. Leading to the logical conclusion that playing learning games that focus on the development of mathematical understanding employs fun, collaboration, and engagement to support learning of mathematics.
Emerald Education’s Elevation Station Games. Fortunately, these arguments for play and gaming do not exist only in the abstract. Emerald Education has created and packaged 135 new Elevation Station Games for K-8 mathematics that embody these opportunities. Each game comes with clear directions, an example of how to play the game, all necessary cards and game boards, and suggested variations that provide for extension and differentiation.
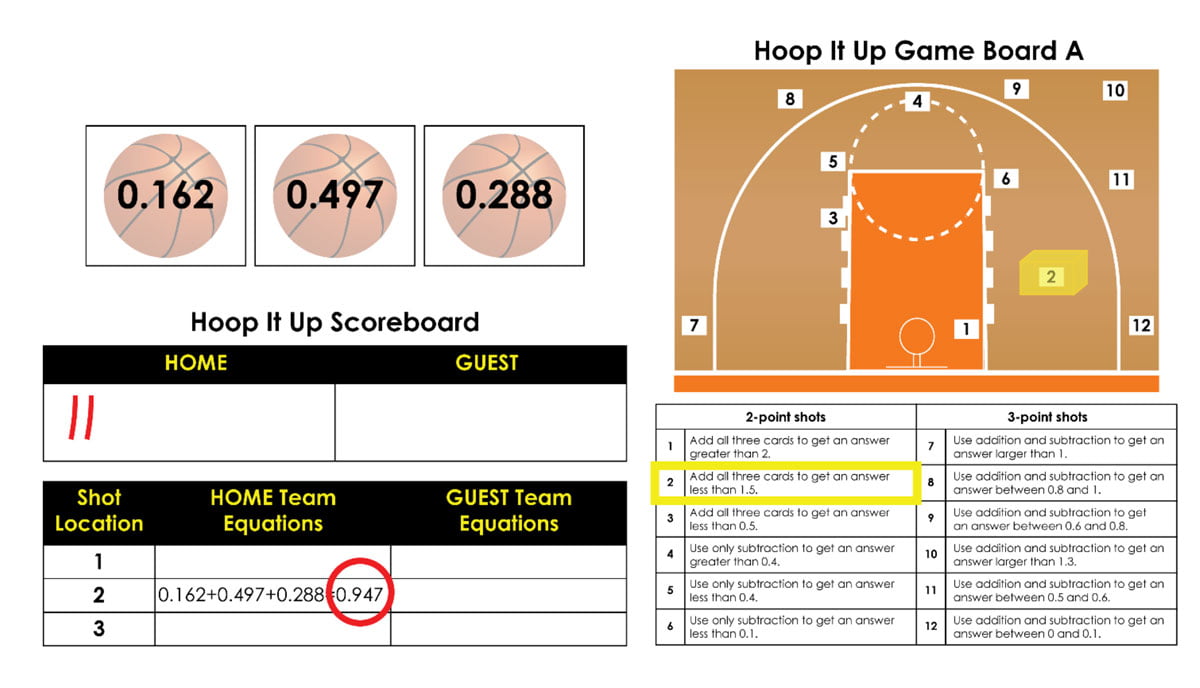
As but one example, consider Hoop It Up – an intriguing cross of basketball, addition and subtraction of decimals, and strategy that incorporates a lot of estimation. The object of the game is to be the first team to score 15 points where teams get 2- or 3- points depending on the “shot” they take and make. Each team gets three decimal cards and alternately take shots selecting from the twelve options on the game board shown below. Once a “shot” is correctly made, that shot location and the specifications for making the shot are no longer available during that round.
Summary. To summarize the case, playing games to support the learning of mathematics promotes:
- the development of mathematical skill and understanding as students engage with the mathematics;
- the development of social skills during game play as students are in situations where collaboration and interaction are necessary;
- the development of work analysis skills as students find it necessary to examine the work of others for accuracy as well as the strategic moves of peers;
- reasoning skills as students navigate and negotiate rules and game play strategies;
- language development as games often require student discourse and justification; and
- the development of resilience in the face of setbacks, challenges, and failures.
These benefits and opportunities present a strong case for incorporating mathematical games into our lessons and Emerald Education has provided us with a powerful 135-game starting place!
